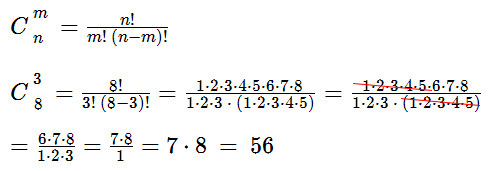в чем выражается цветовая комбинаторика
Организация цветовых построений
Основными формами организации цветовых построений являются: комбинаторика, цветовая фраза, цветовая композиция.


Форма комбинаторики представлена на рис. 17. Выполняя комбинаторику, следует подбирать и менять цвет и расположение элементов мозаики до тех пор, пока цветовое впечатление не окажется самым близким к заданному. Составление комбинаторик — это просмотр цвета. Каждая комбинаторика имеет задачу вовлечь в рассмотрение наибольшее число цветовых сочетаний. Богатство комбинаторики заключается в неповторимости ее элементов. Цветовые комбинаторики дают безотносительную к композиционному замыслу группировку цветов на основе заданных исходных позиции. Комбинаторики позволяют увидеть многочисленные цветовые наборы, и уловить эффект от многих цветовых комбинаций, которые служат для рассмотрения, запоминания, анализа, накопления колористического опыта. Осуществляя «проигрывание» цветовых тонов, комбинаторики могут стать прообразом цветовой композиции.
Упражнения-комбинаторики решают только просмотровые задачи. Более сложные задания выполняются по форме, называемой цветовой фразой. Ее построение должно содержать краткое, но законченное цветовое высказывание, выражающее мысль или чувство автора. Цветовая фраза собирается на сетке из квадратов или строится на основе формальных (абстрактных) цветовых композиций. Цвет и расположение квадратов или цветовых пятен в композиции подбираются по условиям упражнения, с целью организовать нужное цветовое единство. В таком построении цветовой эффект в значительно большей степени зависит от понимания, замысла и вкуса автора, чем в комбинаторике.
В учебных упражнениях, выкраски выкладываются в рассыпные построения, что позволяет просмотреть многие варианты цветовых сочетаний за короткое время. Утвержденные варианты упражнений должны быть зафиксированы, наклеены на листах ватмана формата А-2, А-3 по темам или разделам программы. При оформлении заданий важно правильно разместить материал на листе. Необходимо определить поля и расположить работы так, чтобы им не было «тесно» в листе.
Фиксация найденного цветового результата (в технике аппликации) производится клеем ПВA или резиновым клеем. Вся наклейка должна быть сделана тщательно и аккуратно, чтобы обеспечить чистоту цветового впечатления. Загрязнения и пятна клея не должны попасть на чистовой лист, в случае порчи цветовых выкрасок в упражнении, их следует переделать и наклеить заново.
Работе над цветовым решением формальной композиции всегда предшествует этап предварительных эскизов, и если в композиционной структуре эскизного решения все характеристики заложены принципиально верно, то с ней работают дальше, вводя необходимые детали, делая уточнения и корректировки в соответствии с особенностями конкретной темы. Эскиз в данном случае служит показателем глубины «погружения» в тему, и поэтому в нем важно «схватить» основной образный момент, общий стилистический ход, отобразить грациозность, изящество форм и их пространственные взаимодействия.
«Черновые» варианты композиционных решений выполняются на белой плотной бумаге, предварительно закрепленной на планшете. Это не только создает определенные удобства для работы (твердая и ровная поверхность, минимум деформаций бумаги при работе водяными красками), но и придает аккуратный вид работе, после того как она будет срезана с планшета. Работы выполняются в черно-белой графике.

Комбинаторика в дизайне: сочетания цветов
У каждого человека своё личное восприятие цвета. Каждый по-своему относится к тем или иным цветам и их сочетаниям. Например, для кого-то чёрный — «мрачновато или загробно», а чёрный костюм и автомобиль — это «солидно и круто». Получается, что для кого-то одни цвета и сочетания приятные, а для кого-то нет. И тут начинаются аргументы, почему тот или иной цвет плохой.
Памятка начинающим дизайнерам. Какие цвета нельзя использовать и почему.
Сводная таблица мнений заказчиков. © Fastway
Однажды в магазине я долго листал книгу Михаила Матюшина «Справочник по цвету. Закономерность изменяемости цветовых сочетаний». Внутри есть схемы различных сочетаний цветов, показано их взаимодействие друг с другом, соотношение площадей, залитых цветом. Из-за разницы этих соотношений восприятие цветового сочетания меняется.
Мне очень понравился принцип, по которому строились эти цветовые сочетания и я решил поиграться с цветами. Взял пачку старой цветной бумаги и нарвал из нее кусочков разных размеров в пропорции 1-2-4. А потом наклеил их на листы бумаги. Из трех цветов получилось 6 цветовых сочетаний.
На первый взгляд они все выглядят похоже. Но если посмотреть внимательно, то каждое сочетание создает различное впечатление. Представьте, что это образец обоев, представьте, что так будут выглядеть обои в вашей комнате. Сразу будет понятно, что это давит, это слишком яркое, а это слишком бледное. А вот это вполне ничего.
У меня было 8 цветов в пачке и свободный вечер. Мне стало интересно, сколько вариантов сочетаний цветов можно получить в итоге. Самым простым способом подсчитать варианты было просто их перечислить. В результате перечисления получилось 56 цветовых схем (8 цветов в комбинациях по 3).
Очевидно, что существует формула расчета комбинаций, которую я не знаю. Попробовав различные варианты подсчёта, ничего похожего найти не удалось. С помощью бумажки я стал вести расчет так:
А дальше тяжело. А что если цветов не 8, а больше? Или если в комбинации не три цвета, а два или четыре, или больше? Обратился за помощью к эксперту, и мне быстро подсказали формулу.
Для тех, кто как я, терпеть не мог высшую математику, восклицательный знак в формуле — это факториал. Это означает, что нужно перемножить числа от одного до n. Здесь m — количество цветов в комбинации, n — общее количество цветов.
С помощью этой формулы можно подсчитать любое количество сочетаний и схем. Например, при 3 цветах в схеме и 7 цветах в наборе получится 35 сочетаний, а при 4 цветах в схеме и 10 цветах в наличии получится уже 210 различных сочетаний и т. д.
Interaction of Color — приложение на основе книги и курса по цветоведению американского художника Джозефа Альберса. В нём можно почитать о теории цвета, создавать цветовые комбинации и выполнять упражнения.
Факториал числа n — это произведение всех натуральных чисел от 1 до n включительно. В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества из 4-х элементов существует 4! = 24 перестановки.
Такой же эксперимент можно провести с формой. Пусть у нас будет квадрат 3 × 3, в котором одна клетка другого цвета. Логично, что получится 9 вариантов. А если две клетки другого цвета? То уже 36 вариантов. Если три клетки — 84 варианта. А если увеличить количество клеток другого цвета и в каждой форме закодировать символ, то получится QR-код!
Спросите, зачем всё это? Чтобы представлять себе объём работы. Иногда в процессе работы возникает огромное количество вариантов, на которые тратится драгоценное время. Когда я начал клеить эти бумажки, мне казалось, что это занятие на час, но оно заняло целый вечер и даже не хватило бумаги, чтобы сделать все варианты цветовых сочетаний. 🙂
ABCD, BACD, CABD, DABC
ABDC, BADC, CADB, DACB
ACBD, BCAD, CBAD, DBAC
ACDB, BCDA, CBDA, DBCA
ADBC, BDAC, CDAB, DCAB
ADCB, BDCA, CDBA, DCBA
Наведите свой мобильный телефон на этот код, чтобы добавить меня в свою адресную книгу.
Комбинаторика
Тема 2.5 Комбинаторика. Модуль
Практическая работа 10
Тема 2.4 Контраст. Нюанс. Тождество
Основные понятия:Контраст и его виды: по тону, цвету, насыщенности, фактуре, ассоциациям, форме, конфигурации, массе, направленности движения. Нюанс и тождество, их роль в изобразительном искусстве.
Цель:Находить сходное и различное в сравнительных объектах;
Применять контраст как средство выразительность художественного образа в практических работах.
Нюанс, контраст. Выполнить 2 композиции на сочетании рельефа и графики, используя цвет и фактуру. Формат А5.
Порядок работы над заданием.
Методические указания:
Основные понятия:Комбинаторика. Модуль. Стандарт. Унификация. Биодизайн. Стилизация и трансформация формы. Знак и символ. Приемы стилизации формы. Единая модульная система.
.Комбинации из разных элементов решают люди разных профессий: составление расписания уроков, архитектурная планировка, при решении транспортных задач, составлении шрифтов.
.Комбинаторика- это приемы нахождения различных соединений(комбинаций), перестановок, сочетаний, размещений из данных элементов в определенном порядке.
Ранее других комбинаторный подход проявлялся в строительном деле,и, пройдя через века, сформировался в метод модульного проектирования.
Модуль- это единица меры.
Архитектурный модуль- часть постройки, служащая единицей и используемая для достижения соразмерности здания в целом и его частей.
В классической греческой архитектуре модуль обычно равен радиусу или диаметру колонны у его основания.
Чтобы создать, например, знаменитый кромлех Стоунхендж на территории современной Англии около трёх с половиной тысяч лет тому назад, пришлось изготовить целый набор «типовых» крупноэлементных деталей.
Только для внешнего кольца этого гигантского сооружения понадобилось 30 каменных блоков и 30 каменных плит длиной около трёх с половиной метров.
Сотни тысяч рабов высекали одинаковые каменные блоки в каменоломнях древнего Египта.
На базе модуля строились знаменитые римские водопроводы- акведуки.
Прославленные греческие архитекторы обходились всего тремя типами ордеров и на их основе застраивали целые города.
Характерно, что модулем для жилья в античном мире служил рост человека, те. архитектура древних народов в определенной мере была связана с антропометричностью мер( пядь, фут, локоть, сажень и т. д.
Сейчас наиболее удобным модулем в строительстве признан 0,3 м.=3дм. Это древний фут-длина ступни человека, размер которой одинаково удобен для горизонтальных и вертикальных членений жилого дома.
Теоретические принципы античной модульной системы изложены Витрувием, который считал, что больше всего нужно обращать внимание на пропорциональность здания, соразмерность его с определенной частью, принятой за основную. Основной частью для установления соразмерности ордера служила толщина колонны – её диаметр или радиус. Для стоечно-балочной конструкции отношение диаметра стойки к её высоте играло решающую роль, т. к. определяло устойчивость всей системы.
Греческие архитекторы и свободные ремесленники пользовались модульными пропорциями более творчески, чем римляне, корректируя их соотношения в зависимости от конкретных художественных задач, расположения на местности, абсолютного размера сооружения и т. п.
В 1791 году метр был признан унифицированной единицей длины. В основу единицы длины была положена практически неизменная величина – десятиллиллионная часть четверти парижского меридиана.
Вопрос о переходе на модульную систему в проектировании и промышленности был серьезно поставлен в 20-е годы прошлого столетия. В 1923 году на основе трех госучреждений лесной промышленности организуется акционерное общество «Стандартстрой», которое поставило задачей разработку и постройку типовых жилых и общественных зданий из стандартных конструкционных элементов.
Сама идея стандарта прогрессивна.
Массовое строительство и динамично развивающаяся техника нашего времени столь быстрым темпом изменяют предметную среду, что человеку необходимо осознать, понять и изучить свойства комбинаторных приёмов и широко применять их для её формирования.
Изучение основ комбинаторики стало одной из актуальных задач научно-технического прогресса.
Некоторые композиционные приемы можно продемонстрировать на основе точки, линии и волнистых объемных типоэлементов. На эмоциональное восприятие при этом влияют размеры элементов и их композиционная сочетаемость.
Практическая работа 11Комбинаторные приемы.
Задание: Выполнение раппортных композиций на модульной основе из геометрических фигур (6 эскизов 8×8 см).
Цель:Научиться выполнять работы на модульной основе;Находить комбинаторные элементы на основе геометрических фигур и природных аналогов;
Порядок работы над заданием.
Методические указания:
Использовать треугольники или квадраты в качестве модулей для создания постоянно повторяющегося орнаментального мотива на основе клетчатого раппорта. Для обогащения выразительных средств композиции можно вводить 1-2 цвета, графические фактуры линейного характера, использовать уменьшение и укрупнение модуля.
Стилизация— один из образных приемов, при помощи которого выявляются наиболее характерные черты предмета и отбрасываются ненужные детали. Стилизация бывает по собственным признакам предмета ( колючий ежик) и по привнесенным (мудрая сова).
Трансформация-это изменение формы предмета в необходимую сторону: округление, вытягивание, увеличение или уменьшение в размере отдельных частей, подчеркивание угловатостей и т.д.
Примерами стилизации в графическом дизайне являются знаки и символы. Знак обобщает значительные внешние признаки предмета или только указывает на них.
Знак- это материальный, чувственно воспринимаемый предмет ( явление, событие, действие), выступающий в качестве представителя других предметов ( явлений, событий, действий) и используемый для приобретения, хранения и передачи информации. Первоначально знаки имели материальную природу, но по мере развития общества появились абстрактные знаки, непосредственно связанные с материальной основой( в первую очередь-речь). Все знаки делятся на знаки копии и знаки символы.
ЭМБЛЕМА- это знак, употребление которого является результатом определенного соглашения, договоренности, заключенной в связи с каким-либо общественным историческим обстоятельством (гербы). Как правило, эмблема является сложной комбинацией символов или отдельных их частей.
Практическая работа 12Стилизация природных форм.
Задание:Выполнить стилизацию и трансформацию природной формы. 6-8 эскизов 6×4 см.
Цель:Использовать приемы стилизации в работе.
Порядок работы над заданием.
Методические указания:
Стилизуют обычно с помощью силуэта выраженного пятном, линией или контуром. Силуэт может быть решен, как темным пятном на светлом фоне, так и светлым на темном.. Светлый силуэт на темном фоне должен быть более обобщенным, с меньшим количеством деталей, т.к. он активнее действует на зрителя.
В стилизации отход от натуры( реальной формы объекта) в некоторых случаях бывают очень значительным, например( цветок, облако или насекомое можно трактовать почти как геометрическую форму или преувеличить плавность очертаний их силуэтов. Все наблюдаемые в реальной форме оттенки цвета, при стилизации, как правило сводятся к минимуму цветов, возможен полный отказ от реального цвета. Примером стилизации в декоративно-прикладном искусстве является орнамент.
Для создания оригинального образа можно применить прием стилизации по привнесенным признакам. Для этого следует охарактеризовать предмет по несвойственным ему признакам. Например:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В чем выражается цветовая комбинаторика
1. Элементы комбинаторики.
2. Общие правила комбинаторики.
3. Генеральная совокупность без повторений и выборки без повторений.
4. Применение графов (схем) при решении комбинаторных задач.
1. Комбинаторика и ее возникновение.
Комбинаторика— это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.
Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.
Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок.
Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр.
Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм.
Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д.
2. Общие правила комбинаторики.
Правило суммы: Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m + k способами.
1. Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать?
Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать?
В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть?
Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы.
Правило произведения: Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m *k способами.
1. Сколько двузначных чисел существует?
Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1. Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел.
2. Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»?
3. Генеральная совокупность без повторений и выборки без повторений.
Пример: Набор из n разноцветных лоскутков.
Выборкой объема k ( k n ) называется группа из m элементов данной генеральной совокупности.
Размещениями из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения.
Преобразовав данную формулу, имеем:
Следует помнить, что 0!=1.
1. В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны?
Решение: Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3.
2. Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать?
Решение: Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4.
1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр?
Решение: Имеем перестановки из 5 элементов.
Сочетаниями без повторений из n элементов по k называются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов.
— число сочетаний из n по k
Элементы каждого из сочетаний можно расставить способами. Тогда
1. Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку?
Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3.
Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3.
4. Применение графов (схем) при решении комбинаторных задач.
В случае, когда число возможных выборов на каждом шагу зависит от того, какие элементы были выбраны ранее, можно изобразить процесс составления комбинаций в виде «дерева». Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если на первом шагу был выбран данный элемент и т.д.
Составим соответствующее «дерево».
Ответ: 10 комбинаций.
Такое дерево является графом и применяется для решения комбинаторных задач.